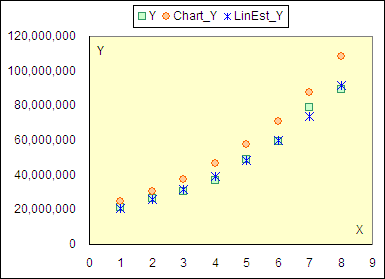
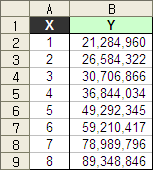
지식iN에 올라온 질문이다. 예제는 아래와 같다.

엑셀에서 분산형 차트를 선택한 후 추세선을 구한다.

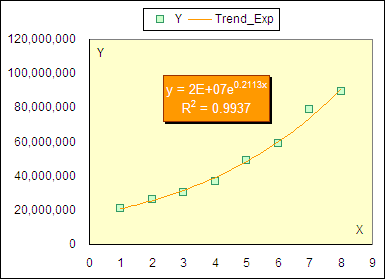
이렇게 구한 회귀계수를 이용해 추정치를 계산한다.

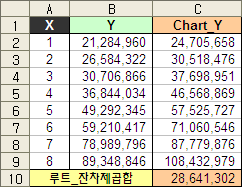
그런데 그래프로 나타내니 추정치가 관찰값과 너무 동떨어져 나타났다고 한다.

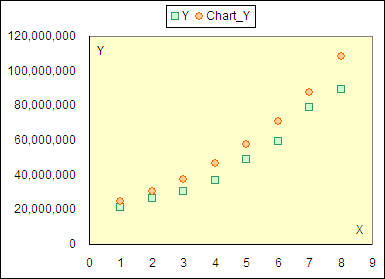
무엇이 문제일까?

계산된 회귀계수와 차트에 나타난 회귀계수 간에 차이가 있으나 이는 엑셀의 오류라기보다는 표시 형식의 제약 때문이다. 회귀계수가 길게 나왔다고 해서 제한된 영역에 모두 표기할 수는 없기에 회귀계수의 표시 형식을 지수로 나타낸 것 뿐이다. 때문에 정확한 결과를 얻고자 한다면 반드시 함수를 이용해 회귀계수나 추정치를 계산해야 한다.

그런데 어느 분이 올린 답변을 보니, 뭐라뭐라 하며 이는 '근사식'이라고 한다. 아마도 비전공자에게 쉽게 말하기 위해 그랬을 수 있지만, 통계에 대한 인식의 한 단면을 보는 것 같아 씁쓸하다.

회귀분석은 종속변수와 독립변수의 관계를 함수로 나타낸 것이다. 이 때 관찰값과 추정치의 차이, 즉 오차는 평균이 0이고 분산이 σ²이며 서로 독립이며 등분산인 정규분포를 따른다고 가정한다.

그리고 회귀모형은 무한대로 존재 가능 하지만, 그 중 가장 작은 오차제곱합을 갖는 유의미한 최적의 회귀모형은 분석자가 찾아내야 한다. 때문에 이는 고된 작업이고 통계 프로그램도 처리할 수 없는 분석자 고유의 영역이다. 그런데 이를 '회귀식'이 아닌 '근사식'이라고 하니... 뭐라 얘기해 줘야할 지 좀 당황스럽다.

아무든 예제에서의 회귀계수와 추정치는 아래와 같다.

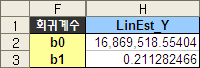
H2 셀(LinEst_Y, b0):

H3 셀(LinEst_Y, b1):

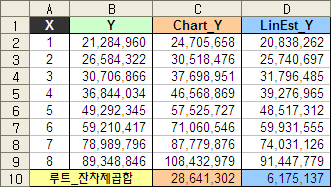
D2 셀(LinEst_Y):