아이엑셀러 닷컴

회귀분석을 돌리면 필히 결정계수를 확인해야 하는데 엑셀에서는 크게 두 가지 방식으로 결정계수를 구할 수 있다. 막강한 LinEst 함수와 단순회귀분석용 RSQ 함수를 이용하면 된다.

아래 자료에 대해 몇 가지 모형을 가정해 추정치를 구해 보았다.

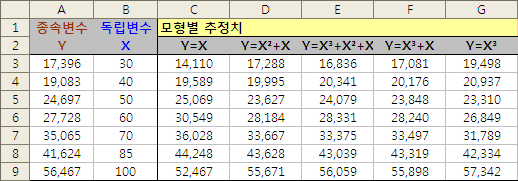
Trend 함수를 활용하면 아래와 같은 방식으로 손쉽게 추정치를 구할 수 있다.

E3 셀(Y=X³+X²+X):
=TREND($A$3:$A$9, $B$3:$B$9 ^ {3, 2, 1}, $B3 ^ {3, 2, 1})

그러면 결정계수는?

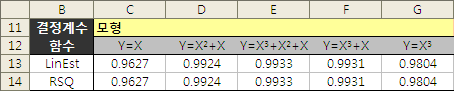
LinEst 함수를 이용해 구하는 방법은 여러 차례 소개했다.

E13 셀(Y=X³+X²+X):
=INDEX(LINEST($A$3:$A$9, $B$3:$B$9 ^ {3, 2, 1}, TRUE, TRUE), 3, 1)

그리고 RSQ 함수는 단순회귀모형에서 간편히 쓰는 함수이나 중회귀모형에서는 앞서 구한 추정치를 가지고 결정계수를 구한다. 물론 결과는 앞에서 구한 것과 같다.

E14 셀(Y=X³+X²+X):
=RSQ($A$3:$A$9, E$3:E$9)

단, 조건이 있다. 위의 방법은 가법모형에 사용하는 방식이고, 승법모형에서는 변수 변환을 해줘야 한다. 대표적 승법모형인 지수 회귀모형을 가정해 구하면,

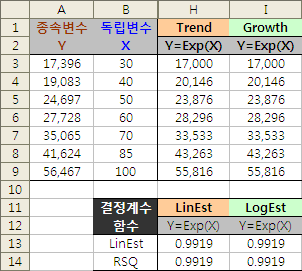
추정치는 변수 변환 후 Trend나 Growth 함수로 구한다.

H3 셀(Trend):
=EXP(TREND(LN($A$3:$A$9), $B$3:$B$9, $B3))

I3 셀(Growth):
=GROWTH($A$3:$A$9, $B$3:$B$9,$B3)

그리고 결정계수는 변수 변환 후 LinEst나 LogEst 함수로 구한다.

H13 셀(LinEst):
=INDEX(LINEST(LN($A$3:$A$9), $B$3:$B$9, TRUE, TRUE), 3, 1)

I13 셀(LogEst):
=INDEX(LOGEST($A$3:$A$9, $B$3:$B$9, TRUE, TRUE), 3, 1)

승법모형에서 RSQ 함수를 이용해 결정계수를 구할 때에는 종속변수뿐만 아니라 추정치에도 변수 변환이 필요하다.

H14 셀:
=RSQ(LN($A$3:$A$9), LN(H$3:H$9))

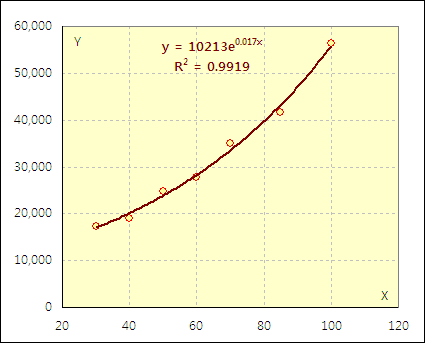
분산형 차트에서 추세선으로도 결정계수를 구할 수 있다. 그러나 이렇게 구한 결정계수는 정확도가 떨어진다는 단점이 있다.

들어가기 전에